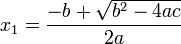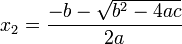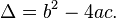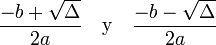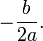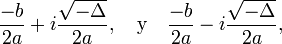Triangulos y Cuadrilateros:

Triangulos:

Se clasifican en:

Equilatero:

Isosceles:

Escaleno:

Tambien se calsifican por sus àngulos como:

Triangulo rectangulo: Tiene un angulo de 90º

Triangulo obtusangulo: Tiene un àngulo mas de 90º

Triangulo acutangulo: Tiene sus àngulos menos de 90º

Criterios de congruencia:

El simbolo que se emplea para denotar la congruencia es

Para comparar dos triangulos y determinar si existe congruencia entre ellos, existen tres criterios, que se describen y ejemplifican a continuacion.

Primer criterio: lado, lado, lado (LLL)

Dos triangulos son congruentes si los tres lados de uno de ellos son congruentes a los lados del otro triangulo.

Segundo criterio: lado, àngulo, lado (LAL)

Dos triangulos son congruentes si, en el primer triangulo, dos de sus lados y el àngulo comprendido entre ellos del segundo triangulo

Tercer criterio: angulo, lado, angulo (ALA)

Dos triangulos son congruentes si dos angulos y el lado comprendido entre ellos, de uno de los triangulos, son congruentes con dos de los angulos y el lado comprendido entre ellos del otro triangulo.

Con la finalidad de ejemplificar los criterios de congruencia de los triangulos.

Solo se puede formar un triangulo si la suma de sus lados es mayor que el tercer lado.

Cuadrilateros:

Se incluyen los trapecios ya que este tiene dos pares de lados paralelos y otros dos que no lo son.

Se definen como paralelogramos:

Tienen al menos dos pares de lados palelos. Dos lados paralelos y cuatro àngulos rectos.

Seclasifican en:

Trapecio isosceles: Los dos lados no paralelos son iguales.

Trapecio rectangulo: Tiene un àngulo de 90º

Rombo: Posee todos sus lados iguales.

Trapezoide: No tiene lados paralelos.

Cuadrado: Todos sus angulos son iguales y tiene cuatro angulos rectos.

Ahora podras observar este power point con la finalidad de aprender con los Triangulos y Cuadrilateros.

En estos Videos encontraras las diferentes formas de los triangulos, sus criterios. Tambien encontraras los cuadrilateros y sus diferentes formas, criterios, etc...

Ecuaciones cuadraticas

En este video encontraras, muchas formas de como hacer o resolver una Ecuaciòn Cuadratrica:

 Ecuaciones cuadraticas.

Una ecuación de segundo grado, ecuación cuadrática o resolvente es una ecuación polinómica donde el mayor exponente es igual a dos. es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:

donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática o parábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).

La formula cuadratica:

Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si los coeficientes son reales y existen dos soluciones no reales, entonces deben ser complejas conjugadas). Se denomina fórmula cuadrática a la ecuación que proporciona las raíces de la ecuación cuadrática:

             

donde el símbolo ± indica que los valores

    y      

Discriminante:
En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):

Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real de multiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.

Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las  abscisas: X):

Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X): 

Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):

donde i es la unidad imaginaria.

En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.

Clasificaciòn:

La ecuación de segundo grado se clasifica de la manera siguiente:

1. Completa. Es la forma canónica:

donde las tres literales: a, b y c, son distintas de cero.

Esta ecuación admite tres maneras para las soluciones: 1) dos números reales y diferentes; 2) dos números reales e iguales (un número real doble); 3) dos números complejos conjugados, según el valor del discriminante

ya sea positivo, cero o negativo, respectivamente.

Se resuelven por factorización, o por el método de completar el cuadrado o por fórmula general. Esta fórmula se deduce más adelante.

2. Incompleta pura. Puede expresarse de las dos maneras siguientes:

donde los valores de a y de c son distintos de cero. Se resuelve despejando x mediante operaciones inversas. Su solución son dos raíces reales que difieren en el signo si los valores de a y de cson de signo contrario, o bien dos números imaginarios puros que difieren en el signo si los valores de a y de c son del mismo signo.

Una ecuación cuadrática incompleta:

con a distinto de cero. Prácticamente aparece muy raras veces. Por supuesto, su única solución de multiplicidad dos es x = 0.

3. Incompleta mixta. Se expresa así:

donde los valores de a y de b son distintos de cero. Se resuelve por factorización de x. Siempre su solución es la trivial x₁ = 0. En números imaginarios no hay solución.

Mètodos para resolver una ecuaciòn:

Factorización:

Para utilizar este método la ecuación cuadrática debe estar igualada a cero.  Luego expresar el lado de la ecuación que no es cero como un producto de factores.  Finalmente se iguala a cero cada factor y se despeja para la variable.

Ejemplos para discusión en clase:  Resuelve las siguientes ecuaciones por factorización:

1)  x² - 4x = 0

2)  x² - 4x = 12

3)  12x² - 17x + 6 = 0

Nota:  No podemos resolver todas las ecuaciones cuadráticas por factorización porque este método está limitado a coeficientes enteros.  Por eso tenemos que conocer otros métodos.

Raíz cuadrada:

Este método requiere el uso de la propiedad que se menciona a continuación.

Propiedad de la raíz cuadrada:  Para cualquier número real k, la ecuación x² = k es equivalente a :

Ejemplos para discusión en clase: Resuelve las siguientes ecuaciones por el método de raíz cuadrada:

1)  x² - 9 = 0

2)  2x² - 1 = 0

3)  (x - 3)² = -8

Completando el cuadrado:

Completar el cuadrado conlleva hallar el tercer término de un trinomio cuadrado perfecto  cuando conocemos los primeros dos.   Esto es, trinomios de la forma: 

x² + bx + ?

Regla para hallar el último término de x² + bx + ?:  El último término de un trinomio cuadrado perfecto ( con a = 1) es el cuadrado de la mitad del coeficiente del término del medio.   Esto es;  el trinomiocuadrado perfecto cuyos dos primeros términos son

 x² + bx  es :

 

Al completar el cuadrado queremos una ecuación equivalente que tenga un trinomio cuadrado perfecto a un lado.  Para obtener la ecuación equivalente el número que completa el cuadrado debe sumarse aambos lados de la ecuación.

Ejemplos para discusión en clase: Resuelve las siguientes ecuaciones por el método de completar el cuadrado:

1)  x² + 6x + 7 = 0

2)  x² – 10x + 5 = 0

3)  2x² - 3x - 4 = 0

Fórmula cuadrática:

La solución de una ecuación ax² + bx + c con a diferente de cero está dada por la fórmula cuadrática:

La expresión:

conocida como el discriminante determina el número y el tipo de soluciones.  La tabla a continuación muestra la información del número de soluciones y el tipo de solución de acuerdo con el valor deldiscriminante.

Valor de:	Tipo de solución
positivo	dos soluciones reales
cero	una solución real
negativo	dos soluciones imaginarias

Ejemplos para discusión en clase:  Resuelve las siguientes ecuaciones cuadráticas usando la fórmula cuadrática:

1)  x² + 8x + 6 = 0

2)  9x² + 6x + 1 = 0

3)  5x² - 4x + 1 = 0

Nota:  Cualquier ecuación cuadrática puede resolverse utilizando la fórmula cuadrática.

Práctica:  Resuelve cada una de las siguientes ecuaciones:

1)  x² - x - 20 = 0    (por factorización)

2)  x² - 8 = 0           (por raíz cuadrada)

3)  x² - 4x + 5 = 0   (completando el cuadrado)

4)  9x² + 6x = 1      (fórmula cuadrática)